I think if you look into tri-planar mapping it might give you some insights in how to approach the problem. Maybe encode the terrain type in the vertex color or normal, and then blend between those in the shader, in a way similar to the tri-planar approach.
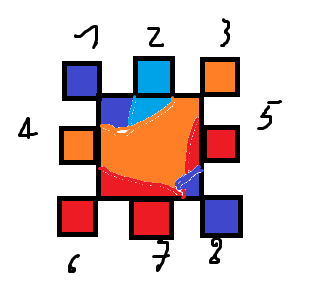
Potentially there are some further simplifications that you could make so that a bunch of static model groups would also work: if the tile down is orange, then divide that time into 9 squares. The center one is fully the color of the tile. The outer ones in the center only have to blend between 2 squares (the top center one blends neighbor 2 and the tile itself). The corner ones then blend 4 tiles (top right would blend 4 tiles: 2, 3, 5, and self). Ignoring rotations, I believe that should be 3 + 3^2 + 3^4 = 93 different sets. If you optimize for rotations and such you can probably reduce the result further (e.g if we’re blending between the same tile types, that is really the same as being fully that tile). One thing to note, you need to decide how you will handle ambiguities - if you have orange on 2 diagonal corners and red on the other two
o r
r o
then which of them will connect in the middle, red or orange?
Also, look into the
marching squares
algorithm, perhaps it will give you additional insight into possible approaches